If we extrapolate from the discussion above to the behavior of pulsars, we see a very compelling picture. By comparison with a pulsar, the Sun is a soft, slow, lumbering affair. It is spread out over a huge volume and rotates only about once a month, and yet the solar cycle, though far from perfect, is still fairly regular. A pulsar, by contrast, is compact, dense, and very fast. In general, we should expect any behavior exhibited by such an object to be considerably less variable—more mathematically perfect—than a comparatively sloppy mess like our sun. The extreme angular velocity of a pulsar combined with its powerful source of gravity (neutron decay) implies an almost incomprehensible pressure difference between its equator and 45° lines. That disparity is half of what drives the magnetic field.
The other half is the Coriolis force, which also driven by rotational velocity, rapidly twists the magnetic lines into strands that are extremely dense. These two dynamics taken together generate an incredibly strong magnetic field, as well as an exceedingly short solar cycle. The field lines are twisted up very quickly and to very high energies. However, they resist breaking until they have reached a much higher energy than those on the Sun because they are responsible for balancing a much higher pressure differential. Finally, when they do break, they release a great deal of energy (their pulses) in a very short span. The energy released is primarily derived from the angular momentum of the star, which is tapped to twist up the field lines. As a result, the magnetic field exerts a kind of friction that gradually slows the star’s rotation.
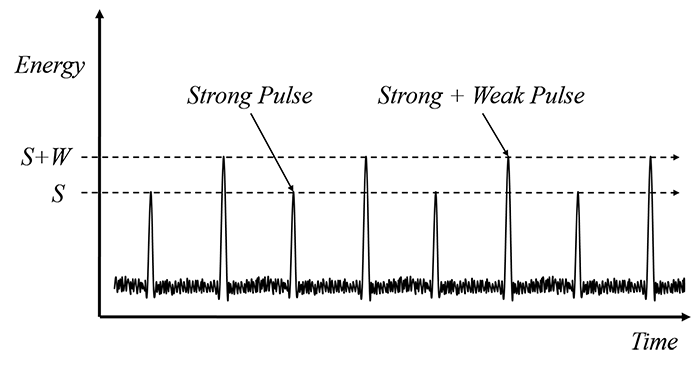
There is also evidence that every other pulse from a pulsar is somewhat more intense than the ones in between (Figure 4.8). If this can be confirmed, it would suggest that the short cycle causes the relatively weak pulses, while the short and long cycles combined cause the relatively strong pulses.
Another point to notice is that if this theory is right, the pulse of a pulsar is not coincident with its rotational period, just as the solar cycle is not coincident with the sun’s rotation. The only reason a pulsar would pulse on each rotation is if it had an asymmetry on one side, like a lighthouse, that was only detectable when it faced us. The currently accepted theory is that the magnetic field of a neutron star looks much like the Earth’s. Since the Earth’s field has poles that are not lined up with its axis of rotation, it is assumed that we can only observe pulsars from which the magnetic poles rotate through our line of sight. However, it is very unlikely that the Earth’s magnetic field is generated the same way as a neutron star’s. The Earth does not liberate spacetime. It is more likely that the Earth’s field is the result of the iron core not rotating in exactly the same plane as the mantle. That is, the solid core of our planet does not track the precession of the axis of the liquid mantle and thin crust, but instead continues rotating in the same plane no matter what the rest of the planet does. If all of this is true, the orientation of a pulsar does not determine whether or not we can observe it.
Now, though the sun’s cycles (11 years and 22 years) are much longer than its rotational period (25 days) there is no reason to assume the same is true of a pulsar. The dynamics that drive the birth and death of magnetic field lines depend on the intensity of the pressure differential and the ability of the force lines to withstand twisting. It remains to be discovered exactly what that might mean for pulsars, but I have a hard time imagining it means they rotate hundreds of times faster than they pulse. There is no doubt they spin very fast, but probably not that fast. As with their gravity, things are not always as they appear with neutron stars.
Articles discussing this section:
Back to the Table of Contents
