Now that we have some familiarity with spacetime and the manner in which it generates gravitational fields, we can turn our attention to another of the great unsolved mysteries of the universe: the curious rotational characteristics of spiral galaxies. Back in the 1930s, a physicist named Fritz Zwicky discovered that objects in spiral galaxies do not seem to observe Newton’s laws. In the 1960s, physicist Vera Rubin took up his work and discovered that objects far away from the center, unlike those in our solar system, do not slow down in proportion to their distance from the core (Figure 4.3).
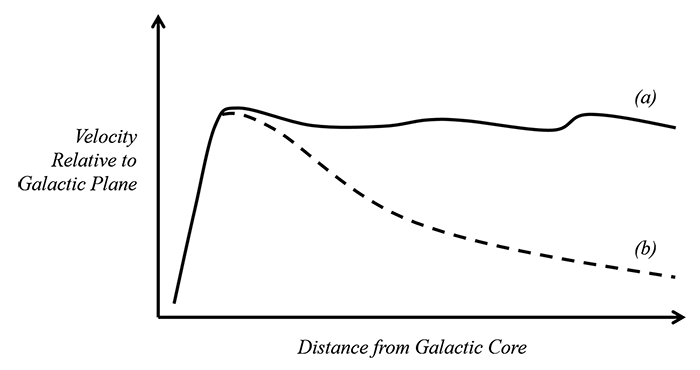
If galaxies behaved according to Newtonian predictions (b), the velocity of objects, relative to the galactic plane, would steadily decrease the farther they are from the core. Instead, it has been observed that objects maintain a nearly constant velocity (a) regardless of their distance.
If our solar system behaved in this way, Neptune’s orbital velocity (5.4 km/sec) would be at least as fast as Mercury’s (48 km/sec), nearly nine times as fast as its true value. So far as Newton is concerned, that would exceed the escape velocity of an object at that distance from the Sun and send it flying off into interstellar space. Nevertheless, that is exactly how it appears to be with our galaxy as a whole. Objects near the rim somehow manage to orbit as rapidly as those near the core without flying off into intergalactic space. This has prompted at least one physicist to speculate that Newton’s laws might change in relation to the velocity of the object under consideration.
Most physicists, to their credit, are hesitant to discard Newton’s laws without a very good reason, but the alternative they have conjured up is no less peculiar. In order to keep the objects at the rim of the Milky Way moving as fast as they do, there must be a very powerful gravitational field that pulls in the opposite direction to the galactic core. Indeed, to account for the motion of our galaxy, the calculated field strength implies a quantity of matter roughly ten times as great as the whole visible galaxy. Unfortunately, when astronomers look they find nothing out there to generate such a field. Therefore, physicists reason, there must be a species of particle that is virtually undetectable, invisible, and only weakly interacting with others of its kind, but which nonetheless exerts a strong gravitational pull. This dark matter—hypothesized to be made of WIMPs (weakly interacting massive particles)—the theory goes, exists as a gigantic halo surrounding the galaxy that exerts exactly the right gravitational counterforce to keep the galaxy rotating the way it does.
If you’re scratching your head and knitting your brow, you are not alone. No direct evidence exists for these WIMPs. Their predicted properties are just whatever is necessary to explain this unexplained phenomenon—not necessarily a bad idea in itself. Unexplained phenomena are great for science; they present an opportunity for discovery. The problem here is that these particular particles are way too convenient. To hold a galaxy in place without tearing it apart, this halo of matter must mold itself into an impossibly unlikely geometric configuration. Also, because galaxies rotate at different velocities and come in different sizes, the quantity of dark matter must exactly balance a specific galaxy’s angular velocity and total mass. That means the quantity of dark matter must be intimately related somehow to the galaxy for which it is responsible. On top of all that, it has to be virtually impossible to detect since, when we point our telescopes at the place where this stuff should be, no one’s home.
Thankfully, there is a perfectly reasonable explanation for galactic rotation that does not require us to either banish Newton or accept the existence of dark matter. As I have shown, all stellar phenomena (stars, black holes, neutron stars, quasars) liberate spacetime in one way or another, either through neutrogenesis, evaporation, or neutron decay. All of this spacetime is liberated by objects that are themselves orbiting the core of the Milky Way at a virtually identical velocity. That is, unlike our solar system, the orbital velocity of all objects in the galaxy is roughly the same and so angular momentumincreases as the distance from the core increases. That, in turn, means the centripetal force required to hold the object in its orbit must also increase. The farther an object is from the galactic core, the harder it pulls against whatever force (I’ll get to that next) is holding it in its orbit. It is easy to see why this is such a confounding problem. The farther an object is from the galactic center, the harder it pulls against the core, despite the fact that gravity ought to decrease the farther one gets from the core. As far as galaxies are concerned, Newton’s laws seem to have been turned upside down. So, what’s the answer?
The centripetal acceleration of any galactic object is related to its orbital radius. By mass, most of these objects are stellar objects, busily churning out spacetime via neutrogenesis, evaporation, or neutron decay. That spacetime, in turn, is liberated into the galaxy with a velocity proportionate to the centripetal acceleration of the object that liberated it. As we saw with black holes, spacetime is very much affected by centripetal acceleration, creating their equatorial bulges. Therefore, spacetime liberated by any stellar object will tend to flow toward the rim of the galaxy at a speed proportionate to the centripetal acceleration of its source. That, in turn, means that the velocity of the spacetime flow at any point in the galaxy is directly proportionate to the distance of that point from the core. Finally, we already know that spacetime resists compression above its equilibrium value. Consequently, as spacetime is accelerated off the edge of the galactic disk, it presses against the cosmos as a whole and, as always, the cosmos pushes right back. This push-back by the cosmos against the flow of spacetime along the disk establishes the cosmological equilibrium of a spiral galaxy. Essentially, spacetime, flowing off the disk, is bottled up and compressed as it attempts to move into intergalactic space. That compression is most intense where the spacetime flow has the highest velocity, namely, near the rim where its source object had the highest centripetal acceleration. As a result, a spacetime pressure gradient (Figure 4.4) is created. It is strongest just outside the rim and gradually diminishes in the direction of the core, as well as way out beyond the rim. A pressure gradient means a gravitational field. It is this phenomenon, not dark matter, that holds the galaxy together.
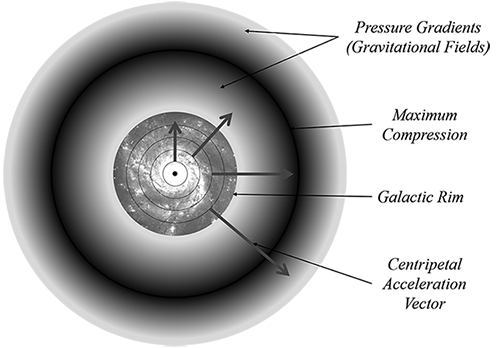
Spacetime accelerated off the rim of a spiral galaxy is compressed as it attempts to move into the intergalactic medium. The resulting pressure gradient creates gravitational fields both inside and outside the ring of maximum compression. This phenomenon, not dark matter, is responsible for galactic rotation as well as gravitational lensing.
The evidence for this model is overwhelming. Notice that no matter what the rotational velocity of a given galaxy, no matter how rapidly or slowly it spins, and no matter how massive it is, the strength of the resulting gravitational field will always be exactly calibrated to hold it together. This is because the centripetal accelerations of the sources of spacetime are proportionate to their angular velocities, and the intensity of the spacetime gradient is, in turn, proportionate to centripetal accelerations of its various stellar sources. These variables, whatever they happen to be, always find a stable cosmological equilibrium. The spacetime flowing off the edge of the disk pushes against the cosmos in proportion to the angular velocity of the galaxy, and that is what determines the intensity of the gravitational field (the spacetime pressure gradient). Notice also that the intensity of the gravitational field at any point in the galaxy is proportionate to the radius at that point, meaning that the field strength decreases smoothly toward the core. A giant mass of dark matter would tend to pull the galaxy into a ring or donut shape unless its physical distribution and consequent gravitational pull just happened to correlate exactly with the disk shape we actually observe, and that would be very hard to explain. Neither do we have to explain how exactly the right quantity of dark matter happens to be present to generate the proper gravitational field for any particular galaxy.
Another piece of evidence: Draw a line from the galactic core through the earth and on to the rim (Figure 4.5). If we measure the Doppler shift of starlight anywhere along this segment, we find that it is directly proportionate to the difference between the velocity of the spacetime flow at that point and its velocity here at earth. Starlight is red-shifted anywhere along the segment between the earth and the core and blue-shifted between the earth and the rim. Moreover, the extent of the blue shift increases as the star in question approaches the rim. This happens because the light from blue-shifted stars must flow upstream against the spacetime current and is compressed in the process, shortening its wavelength. Meanwhile, light from red-shifted stars is stretched. These Doppler shifts have little to do with the relative motions of the stars. Stars near the rim are not moving much, if at all, toward the earth, despite their blue-shifted light.

Starlight reaching the earth is red-shifted if its source is between the earth and the galactic core, and blue-shifted if it comes from a star between the earth and the rim. The flow of spacetime toward the rim of the galaxy, not the relative motions of the stars, is primarily responsible for this Doppler effect.
Finally, this galactic gravitational field is shaped like a large flattened out donut with the thickest part just beyond the rim. In essence, it is a huge circular convex lens that, not coincidentally, is exactly the necessary shape to account for the gravitational lensing that astronomers have observed.
Articles discussing this section:
Back to the Table of Contents
